年輕的俄羅斯數(shù)學(xué)家羅巴切夫斯基突發(fā)奇想，將古老歐氏平面幾何的“平行公理”稍作改變，創(chuàng)立了邏輯上同樣完整而嚴(yán)密，但看起來(lái)卻有些古怪的“非歐幾何”。最初，人們對(duì)此嗤之以鼻，認(rèn)為這不過(guò)是瘋子數(shù)學(xué)家玩的游戲而已。

不過(guò)，那些嘲笑羅巴切夫斯基的人沒(méi)有料到，幾十年之后，非歐幾何在愛(ài)因斯坦的廣義相對(duì)論中找到了用武之地。它正是廣義相對(duì)論中描述的一種彎曲空間所遵循的幾何！

古老的幾何學(xué)

幾何是一門(mén)古老的學(xué)科，在公元前由幾何大師歐幾里德創(chuàng)立，至今兩千多年威力不減。

歐幾里德幾何是一個(gè)漂亮的公理系統(tǒng)，它只需要設(shè)定幾條簡(jiǎn)單的、符合直覺(jué)、大家公認(rèn)、不證自明的命題（稱為公理或公設(shè)），然后從這幾條命題出發(fā)，推導(dǎo)證明其它命題，繼而推導(dǎo)證明更多命題，如此繼續(xù)下去，一套數(shù)學(xué)理論便建立起來(lái)了。這就像是建造高樓大廈，“公理”就是水平放在地基第一層的大“磚塊”，有了牢靠堅(jiān)實(shí)的基礎(chǔ)，其它磚塊便能夠一層一層疊上去，萬(wàn)丈高樓也就能夠平地而起。基底磚塊破缺了，或者置放得不平穩(wěn)，樓房就可能會(huì)倒塌。

歐幾里德平面幾何的公理有五條。他就從這簡(jiǎn)單的五條公理出發(fā)，推演出了所有的平面幾何定理，建造出歐氏幾何的宏偉大廈。

數(shù)學(xué)邏輯推理創(chuàng)造的奇跡令人吃驚。不過(guò)，當(dāng)人們反復(fù)思考這幾條公理時(shí)，覺(jué)得前面4條顯然都是不言自明的，唯有第五條公理比較復(fù)雜，聽(tīng)起來(lái)不像一個(gè)簡(jiǎn)單而容易被人接受的直覺(jué)概念。于是，人們就自然提出疑問(wèn)：這第五條是公理嗎？它是否可以由其它4條公理推導(dǎo)出來(lái)？大家的意思就是說(shuō)，歐氏平面幾何的大廈用前面4塊“大磚頭”可能也就足以支撐了。這第五塊磚頭，恐怕本來(lái)就是放置在另外四塊磚頭之上的。

歐氏平面幾何的第五條公理也稱為“平行公理”，可表述為：“過(guò)直線外的一點(diǎn)，有且僅有一條平行線。”

一位名叫尼古拉·羅巴切夫斯基（Nikolai Lobachevsky，1792 - 1856）的年輕俄羅斯數(shù)學(xué)家突發(fā)奇想：如果將這條公理稍稍改變一下，也就是說(shuō)，將大廈下面的某塊基石稍微移動(dòng)一下，會(huì)產(chǎn)生什么樣的后果呢？比如說(shuō)改成：“過(guò)直線外的一點(diǎn)，至少有兩條平行線。”

這一改非同小可，幾字之差，生出了與歐氏幾何完全不同的另一種幾何，人們稱之為“非歐幾何”或“羅氏幾何”。非歐幾何的大廈同樣拔地而起、穩(wěn)固牢靠，邏輯上完整而嚴(yán)密，但看起來(lái)卻有些古怪。

羅氏幾何體系得到古怪而不合常理的命題是必然的，因?yàn)楸涣_巴切夫斯基改變之后的第五公設(shè)，本身就與人們的日常生活經(jīng)驗(yàn)不相符合。過(guò)平面上直線外的一點(diǎn)，怎么可能作出多條不同的直線與已知直線不相交呢？由此而建造出來(lái)的數(shù)學(xué)邏輯大廈，當(dāng)然會(huì)是個(gè)怪物。比如說(shuō)，羅氏幾何導(dǎo)出了如下古怪的命題：同一直線的垂線和斜線不一定相交；不存在矩形，因?yàn)樗倪呅尾豢赡芩膫€(gè)角都是直角；不存在相似三角形；過(guò)不在同一直線上的三點(diǎn)，不一定能作一個(gè)圓；一個(gè)三角形的三個(gè)內(nèi)角之和小于180度……這種奇怪的“幾何大廈”，能有什么用處呢？有人嗤之以鼻，心想，不過(guò)是瘋子數(shù)學(xué)家玩的游戲而已！

那些嘲笑羅巴切夫斯基的人沒(méi)有料到，幾十年之后，非歐幾何在愛(ài)因斯坦的廣義相對(duì)論中找到了用武之地，它正是愛(ài)因斯坦廣義相對(duì)論描述的一種彎曲空間所遵循的幾何！

幾何上的無(wú)窮小

不過(guò)，真正與廣義相對(duì)論彎曲空間有關(guān)的是“黎曼幾何”，它比上面所說(shuō)的非歐幾何更進(jìn)了一步，屬于微分幾何。

歐幾里德之后，笛卡爾發(fā)明了解析幾何，牛頓和萊布尼茨發(fā)明了微積分。兩者之結(jié)合使得那個(gè)時(shí)代的數(shù)學(xué)和物理如虎添翼，面目一新。像羅巴切夫斯基那樣使用傳統(tǒng)的公理方法來(lái)研究幾何，顯然要輸人一籌。歐拉、克萊洛、蒙日以及高斯等人認(rèn)識(shí)到了這一點(diǎn)，創(chuàng)立并發(fā)展了微分幾何。

微分幾何的先行者、法國(guó)數(shù)學(xué)家亞歷克西斯·克萊洛（Alexis Clairaut，1713 - 1763）對(duì)空間曲線進(jìn)行了深入研究，第一次研究了空間曲線的曲率和撓率（當(dāng)時(shí)被他稱之為雙重曲率）。

什么是曲線的曲率和撓率？我們從圖1a所示的三條平面曲線來(lái)認(rèn)識(shí)曲率。圖中的三條曲線，就像是三條形狀不同的平地上的高速公路。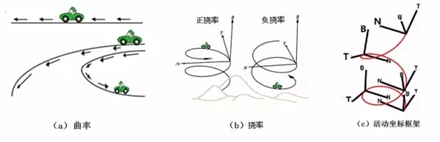

我們首先需要引進(jìn)曲線的切線，或稱之為“切矢量”的概念。切矢量即為，當(dāng)曲線上兩點(diǎn)無(wú)限接近時(shí)，它們的連線的極限位置所決定的矢量。圖1a所示的公路上標(biāo)示的箭頭，便是在曲線上各個(gè)點(diǎn)切矢量的直觀圖像。而曲率是什么呢？曲率表征曲線的彎曲程度。比如，圖1a中最上面一條公路是直線，直線不會(huì)拐彎，我們說(shuō)，它的彎曲程度為0，即曲率等于0。切矢量旋轉(zhuǎn)得越快，曲線的彎曲程度也越大。所以，數(shù)學(xué)上就把曲率定義為曲線的切矢量對(duì)于弧長(zhǎng)的旋轉(zhuǎn)速度。

平地上彎彎曲曲的公路可以看作是平面曲線，用“曲率”就可以描述它們。如果公路是修建在山區(qū)中，它們一邊轉(zhuǎn)彎一邊還要盤(pán)旋向上或者向下。這時(shí)候，汽車(chē)駛過(guò)的路徑便不再是平面曲線，而是空間曲線了。對(duì)于山間的公路，如圖1b所示，我們除了可以看到其彎曲的程度之外，還能觀察到公路往上（或者向下）繞行的快慢。我們將這個(gè)描述繞行快慢的幾何量叫做“撓率”。

一條空間曲線的曲率和撓率在空間的變化規(guī)律完全決定了這條曲線。

從上面對(duì)空間曲線的研究，可以看出微分幾何的方法比歐氏幾何公理式的方法要強(qiáng)有力多了。與曲線類(lèi)似，微分幾何也能用以研究曲面，曲率和撓率的概念，也能推廣到曲面上，去定義復(fù)雜得多的曲率張量。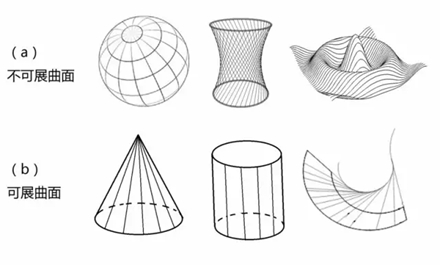

曲面的形狀變幻無(wú)窮，按照我們感興趣的性質(zhì)，可以將其分為兩大類(lèi)：可展曲面和不可展曲面。初看圖2a和圖2b所畫(huà)出的曲面，也許你看不出這兩類(lèi)圖形有何區(qū)別。它們都是從三維空間看到的形狀。不管可展還是不可展，看起來(lái)不都是“彎曲的”、“不平的”嗎？然而，如果你再仔細(xì)觀察，就會(huì)發(fā)現(xiàn)，可展曲面的“彎曲”與不可展曲面的“彎曲”有著本質(zhì)的區(qū)別。簡(jiǎn)單地說(shuō)，可展曲面在本質(zhì)上是“平的”，它們可以被展開(kāi)成一個(gè)平面。比如，將圖2b所示的錐面，用剪刀剪一條線直到頂點(diǎn)，就可以沒(méi)有任何皺褶地將它平攤到桌子上。柱面也可以沿著與中心線平行的任何直線剪開(kāi)，成為一個(gè)平面。

但是，圖2a所列舉的不可展曲面，就不能展開(kāi)成平面了。那是真正的、本質(zhì)上的“不平”。一頂做成了近似半個(gè)球面的帽子，你無(wú)論怎樣剪裁它，都無(wú)法將其沒(méi)有皺褶地?cái)偝梢粋€(gè)平面。另一方面，你用一張平平的紙，很容易卷成一個(gè)圓筒（柱面），或者是做成一頂錐形的帽子，但你無(wú)法做出一個(gè)球面來(lái)。你頂多只能將這張紙剪成許多小紙片，粘成一個(gè)近似的球面！

談到這兒，你大概已經(jīng)基本明白了“可展”和“不可展”的區(qū)別到底是什么。盡管兩類(lèi)曲面在嵌入3維空間之后看起來(lái)都是彎曲的，但是，可展曲面的內(nèi)在本質(zhì)是“平的”，不可展曲面的內(nèi)在本質(zhì)是“不平”。區(qū)分這兩類(lèi)曲面“內(nèi)在本質(zhì)”的概念叫做“內(nèi)蘊(yùn)性”，研究這種性質(zhì)的幾何叫做內(nèi)蘊(yùn)幾何。

曲面彎曲的內(nèi)蘊(yùn)性最早被“數(shù)學(xué)王子”高斯注意到，后為黎曼所發(fā)展，并推廣到大于3的n維流形。因而，黎曼幾何是一種內(nèi)蘊(yùn)幾何。換言之，內(nèi)蘊(yùn)性指的是曲面（或曲線）不依賴于它在三維空間中嵌入方式的某些性質(zhì)。也就是說(shuō)，它是曲面某些內(nèi)在的、本質(zhì)的幾何屬性。高斯用高斯曲率——兩個(gè)主曲率的乘積，來(lái)表征曲面的這種屬性（圖3a）。如果一個(gè)曲面的高斯曲率為0，說(shuō)明它本質(zhì)上是平的，是可展曲面，如圖3b所示。如果一個(gè)曲面的高斯曲率不為0，說(shuō)明它本質(zhì)上是不平的，是不可展曲面，如圖3c所示。

高斯曲率不為0的情形又有兩種。正的高斯曲率對(duì)應(yīng)于球面幾何（圖3c的下圖），負(fù)的高斯曲率對(duì)應(yīng)于馬鞍面（圖3c的上圖）。馬鞍面上的幾何就是前面所介紹的羅巴切夫斯基幾何，又被稱為雙曲幾何。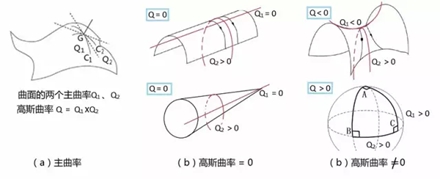

爬蟲(chóng)的幾何

可是，又該如何判定我們所面對(duì)的是哪一種幾何呢？最簡(jiǎn)單的辦法是測(cè)量曲面上一個(gè)三角形三個(gè)內(nèi)角之和E=A+B+C。平面幾何的E=180o，球面幾何E>180o，雙曲幾何E<180o。

一個(gè)觀察者在自己生活的物理空間中所能夠觀察和測(cè)量到的幾何性質(zhì)，就是這個(gè)空間的內(nèi)蘊(yùn)性質(zhì)。比如說(shuō)，球面的內(nèi)蘊(yùn)性質(zhì)，就是生活在球面上的2維爬蟲(chóng)感受到的幾何性質(zhì)。我們?nèi)祟?lèi)當(dāng)然是3維的生物，不是什么2維爬蟲(chóng)。但是，因?yàn)槲覀兊牡厍蚝艽螅覀兊?維尺寸比起地球來(lái)說(shuō)是很小的。因此，我們可以將自己設(shè)想為某種2維生物。比如，我們?cè)诘厍蛏蠝y(cè)量一個(gè)大三角形，就如圖3b下中的球面三角形ABC，測(cè)地員將會(huì)發(fā)現(xiàn)，這個(gè)三角形的三個(gè)內(nèi)角都是90度，因此，內(nèi)角和E=270o，大于180度。

圖3b下所顯示的是一個(gè)規(guī)則球面，它的空間彎曲程度到處都是一樣的，但一般來(lái)說(shuō)，空間的彎曲程度不一定處處相同，數(shù)學(xué)家們用“平行移動(dòng)”的概念來(lái)研究空間的彎曲程度。

什么是平行移動(dòng)？簡(jiǎn)單地說(shuō)，就是將一個(gè)矢量平行于自身的方向沿著空間里的一條曲線移動(dòng)。像汽車(chē)上的陀螺儀那樣，汽車(chē)沿公路運(yùn)動(dòng)時(shí)，陀螺儀總是平行于自己原來(lái)的指向。

在物理上，讓大家更感興趣的問(wèn)題是：一個(gè)矢量平行移動(dòng)一圈后再回到原來(lái)出發(fā)點(diǎn)的時(shí)候是否會(huì)有所改變？比如說(shuō)，跟著汽車(chē)轉(zhuǎn)了一圈的陀螺儀，指的方向是否還和原來(lái)出發(fā)時(shí)的方向一樣？也許你不加思索就會(huì)給出答案：當(dāng)然沒(méi)有什么改變。但這是因?yàn)槟懔?xí)慣了用歐氏空間的直角坐標(biāo)系來(lái)思考問(wèn)題，從而輕易得出這個(gè)結(jié)論。如果我們假設(shè)地面是一個(gè)歐幾里德平面，陀螺儀平行移動(dòng)回到原處時(shí)，方向的確不會(huì)改變。但是，每個(gè)人都知道，地球是一個(gè)球體，所以我們實(shí)際上是生活在一個(gè)球面上。那么，如果從球面（或者別的曲面）的角度來(lái)研究這個(gè)問(wèn)題，又會(huì)得出什么樣的結(jié)論呢？

所謂“平行移動(dòng)”的意思是說(shuō)，在移動(dòng)矢量的時(shí)候，盡可能保持矢量方向相對(duì)于自身沒(méi)有旋轉(zhuǎn)。好比一個(gè)女孩平行地前進(jìn)、后退、左右移動(dòng)，只要她的身體沒(méi)有扭動(dòng)，就叫平行移動(dòng)。這樣，當(dāng)她移動(dòng)一周回到出發(fā)點(diǎn)的時(shí)候，她認(rèn)為她應(yīng)該和原來(lái)出發(fā)時(shí)面對(duì)著同樣的方向。如果她是在平面上移動(dòng)的話，她的這個(gè)想法是正確的。但是，假如她是在球面上移動(dòng)的話，她將發(fā)現(xiàn)自己面朝的方向可能不一樣了！出發(fā)時(shí)她的臉朝左，回來(lái)時(shí)卻是臉朝前，如圖4b。

假如將女孩面對(duì)的方向用一個(gè)箭頭（矢量）來(lái)表示。圖4a所示的是一個(gè)矢量在莫比烏斯帶上的平行移動(dòng)，當(dāng)矢量從位置1出發(fā)，沿著數(shù)字1、2、3……一直移動(dòng)到10，也就是回到原來(lái)的出發(fā)位置時(shí)，得到的矢量和原來(lái)的反向。圖4b中所示是球面上的平行移動(dòng)，當(dāng)矢量從位置1出發(fā)，沿著數(shù)字1、2、3……一直移動(dòng)到7，也就是回到原來(lái)的出發(fā)位置時(shí)，得到的矢量和原來(lái)的矢量垂直。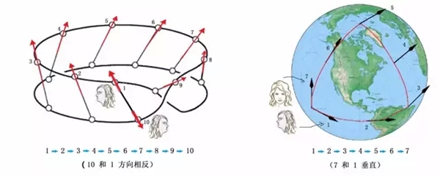

上面的兩個(gè)例子說(shuō)明，矢量在曲面上平行移動(dòng)一周之后，不一定還能保持原來(lái)的方向，可能與出發(fā)時(shí)有所差別。這個(gè)差別正好與曲面的高斯曲率有關(guān)系，反映了曲面內(nèi)在的彎曲程度。

阿扁的世界

下面，我們研究錐面上的平行移動(dòng)，看看錐面與“真正的平面”有何不同。讓我們想象有一個(gè)極小極扁的平面生物“阿扁”，生活在一張平坦的紙上，如圖5a。阿扁使用直角坐標(biāo)系對(duì)他的平坦世界進(jìn)行觀察和測(cè)量。他感受到的幾何，是標(biāo)準(zhǔn)的歐幾里德幾何：三角形的三個(gè)內(nèi)角之和等于180度；過(guò)不在同一直線上的三點(diǎn)，可以作一個(gè)圓；直角三角形的兩條直角邊的長(zhǎng)度的平方和等于斜邊長(zhǎng)的平方……

阿扁學(xué)過(guò)微積分，還會(huì)計(jì)算許多圖形的面積。阿扁經(jīng)常在他的平坦世界中駕車(chē)旅行，繞行一圈回來(lái)之后，他車(chē)上的陀螺儀方向總是與原來(lái)方向相同，如圖5a所示的那樣。

有一天，來(lái)了一個(gè)3維世界的小生物“阿三”。阿三看中了阿扁生活的這張紙，并且靈感突發(fā)，把這張紙剪去了一個(gè)角。比如說(shuō)，像圖5b中圖所畫(huà)的情形，剪去了一個(gè)45度的角，然后將剩余圖形的兩條剪縫黏在一塊兒，做成了一個(gè)圖5c所示的錐面。阿扁是個(gè)2維小爬蟲(chóng)，他看不見(jiàn)阿三，也感覺(jué)不到阿三的存在，更不可能知道阿三對(duì)他的世界干了些什么。

不過(guò)，生活在紙上的阿扁并沒(méi)有立即感到他的世界有什么變化。照樣是歐氏幾何，他畫(huà)的直角坐標(biāo)軸仍然在那兒。當(dāng)他拿著他的（平面）陀螺儀，沿著他的小圓圈（如圖5b中的C1那樣）旅行，進(jìn)而回到原來(lái)出發(fā)點(diǎn)的時(shí)候，陀螺儀的指向和原來(lái)一樣。這說(shuō)明，矢量平行移動(dòng)的規(guī)律好像沒(méi)有任何改變。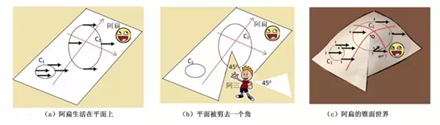

阿扁的技術(shù)越來(lái)越高，膽子越來(lái)越大，旅游路線也走得越來(lái)越遠(yuǎn)。他逐漸發(fā)現(xiàn)了一些問(wèn)題。比如說(shuō)，當(dāng)他沿著圖5b中所示的C2那樣的曲線走一圈回到原出發(fā)點(diǎn)時(shí)，他的陀螺儀的指向和出發(fā)時(shí)有了一個(gè)45度的角度差。這個(gè)新發(fā)現(xiàn)令阿扁既激動(dòng)又困惑。于是，他進(jìn)行了更多的帶陀螺儀繞圈實(shí)驗(yàn)，繞了好多個(gè)不同的圈，終于總結(jié)出了一個(gè)規(guī)律：他生活的世界中，在右圖中所標(biāo)記的點(diǎn)O附近，是一個(gè)特殊的區(qū)域，只要他移動(dòng)的閉曲線中包含了這個(gè)區(qū)域，陀螺儀的指向就總是和原來(lái)出發(fā)時(shí)的方向相差45度左右。如果行走的圈沒(méi)有包括這個(gè)點(diǎn)的話，便不會(huì)使陀螺儀的方向發(fā)生任何改變。當(dāng)時(shí)的阿扁，技術(shù)還不夠精確，還沒(méi)有搞清楚這個(gè)區(qū)域是多大，況且，他也有點(diǎn)害怕那塊神秘兮兮的地方，不敢在那兒逗留過(guò)久，作太多的探索，以防遭遇生命危險(xiǎn)。

阿扁喜歡讀書(shū)學(xué)習(xí)新知識(shí)，他從一本數(shù)學(xué)書(shū)中了解到，如果陀螺儀走一圈方向改變的話，說(shuō)明你所在的空間是彎曲的。因此，通過(guò)對(duì)多次實(shí)驗(yàn)結(jié)果的總結(jié)歸納，阿扁提出一個(gè)假設(shè)：他所在的世界基本是平坦的，除了那塊該死的區(qū)域之外！

再回到我們的世界來(lái)看待球面幾何。陀螺儀走一圈后方向改變的值，叫做平行移動(dòng)一周后產(chǎn)生的角度虧損，可用θ表示。角度虧損與空間的高斯曲率有關(guān)，一個(gè)標(biāo)準(zhǔn)球面上的高斯曲率處處相等。因此，如果有某種生活在球面上的扁平生物的話，他沿任何曲線繞行一圈后，陀螺儀方向都會(huì)有變化，而且，角度虧損θ是不固定的，它與繞行回路所包圍的球面面積A成正比，其比例系數(shù)對(duì)球面而言是一個(gè)定植，就等于曲面的高斯曲率α。角度虧損θ = α*A。

如果研究對(duì)象不是標(biāo)準(zhǔn)的球面，而是一般的2維曲面，上述“角度虧損θ正比于區(qū)域面積A”的結(jié)論在大范圍內(nèi)不能成立，但在2維曲面某個(gè)給定的P點(diǎn)附近，當(dāng)繞行的回路趨近于無(wú)限小的時(shí)候仍然成立。也就是說(shuō)：無(wú)限小的角度虧損dθ將正比于無(wú)限小的區(qū)域面積dA：dθ = α*dA。這時(shí)的α= dθ/dA，便是曲面上這一點(diǎn)的曲率。

阿扁也想通了這些道理，明白他的世界不是球面，而大多數(shù)地方都是平面，只有一點(diǎn)不對(duì)，那一點(diǎn)附近的空間是彎曲的。

阿扁將上面有關(guān)曲面曲率與無(wú)限小平行移動(dòng)角度虧損的關(guān)系（α= dθ/dA）用到錐面。因?yàn)殄F面是一個(gè)可展曲面。它所有地方的幾何都與平面上的歐幾里德幾何一樣，除了那個(gè)頂點(diǎn)以外。也就是說(shuō)，錐面上每個(gè)點(diǎn)的曲率都等于0，但頂點(diǎn)是一個(gè)曲率等于無(wú)窮大的奇點(diǎn)。

有了這些數(shù)學(xué)知識(shí)，阿扁恍然大悟：原來(lái)我生活的世界是一個(gè)錐面！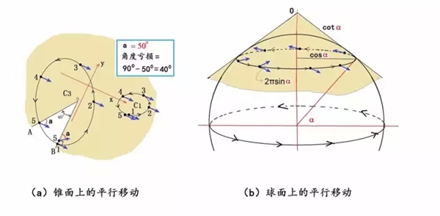

人類(lèi)是三維空間的生物，我們的世界是三維的。就像前面所描述的“阿三”，當(dāng)然要比那個(gè)可憐的平面生物“阿扁”高明多了。阿扁反復(fù)測(cè)量了許多次，用他的2維扁平腦袋，作了極端困難的“抽象”，才弄明白了他的錐面世界！而我們?cè)?維世界中看2維就能看得非常清楚了：錐面是一個(gè)可展曲面，或者說(shuō)，本來(lái)就是由阿三將一張平面的“紙”剪去了一個(gè)角而粘成的。因此，我們瞄一眼就知道，阿扁的錐面世界處處都是平坦的，除了那一個(gè)頂點(diǎn)O之外。

在錐面上作平行移動(dòng)時(shí)，為什么當(dāng)移動(dòng)路徑包括了頂點(diǎn)O的時(shí)候就會(huì)有角度虧損呢？從我們的3維世界更容易理解這個(gè)問(wèn)題。在圖6a中，我們將錐面從頂點(diǎn)剪開(kāi)后重新展開(kāi)還原成一個(gè)平面圖形。這個(gè)“剪去一角的平面圖形”與整個(gè)歐幾里德平面的區(qū)別在于，圖中的A和B是錐面上的同一點(diǎn)，因此，直線OA和OB需要被理解為是同一條線。這樣，我們就明白了角度虧損的來(lái)源。

（作者：張?zhí)烊兀驴怂_斯州大學(xué)奧斯汀分校理論物理博士）